Random Hyperbolic Graphs

During a 4-months internship (April to July 2018), I studied propagation models into Random Hyperbolic Graphs at Laboratoire J.A. Dieudonné (Université Nice Côte d’Azur). I was supervised by Dieter Mitsche.

Random Hyperbolic Graphs

Random hyperbolic graphs are a generalisation of random geometric graphs in hyperbolic spaces. Random geometric graphs have nodes uniformly generated in some part of the Euclidean space and two vertices are connected by an edge if and only if the euclidian distance between both is less or equal to a fixed threshold which is a parameter of the model. Edges of random hyperbolic graphs are following the same rule, except that the distance used to generate edges is the hyperbolic distance $\text{dH}$ in a hyperbolic space of negative curvature.

Let $\alpha, \nu > 0$ and $n \in \mathbb{N}$. Fixing $R := 2 \log (n / \nu)$, we say that a graph $\mathcal{G}_{\alpha, ~\nu} (n) := (V, E)$ (with $|V| = n$) is a random hyperbolic graph if:

• the vertices $v_1, \dots, v_n$ of $V$ are independently generated in $\mathbb{B}(O, R)$ with density $$ f : \mathbb{R}_+ \times [0, 2\pi[ \to \mathbb{R}, \quad (r, \theta) \mapsto \frac{\rho(r)}{2\pi} \quad \text{where} \quad \rho(r) = \frac{\alpha \sinh(\alpha r)}{\cosh(\alpha R) - 1} \textbf{1} (r \in [0, R])$$ (the radial and angular coordinates $r$ and $\theta$ of each vertice are independent, $r$ generated with density $\rho$ and $\theta$ uniformly chosen in $[0, 2\pi[$),

• the edge set $E$ is entirely determined by the positions of the vertices, that is to say that two vertices $u, v \in V$ are adjacents if and only if $\text{dH} (u, v) \leq R$: $$ u \leftrightarrow v \in E \quad \Leftrightarrow \quad \text{dH} (u, v) \leq R $$

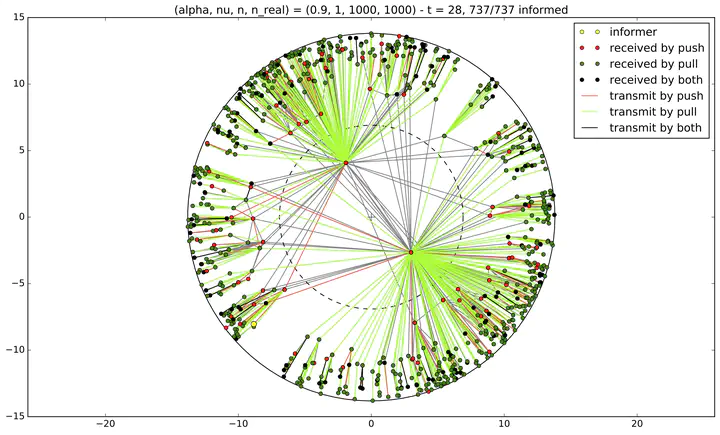
Push & Pull propagation

I studied a rumor spreading model: the push & pull model. Starting by randomly choosing a vertex which is the first informed at time $t=0$, at each time two processes happen simultaneously and independently:

• a push: each informed vertex chooses one of its neighbours uniformly and transmits it the information if it did not already have it,
• a pull: each non-informed vertex chooses one of its neighbours uniformly. It receives the information if this neighbour already has it.

Our goal was to find the average time needed to inform the whole giant component of $\mathcal{G}_{\alpha,~\nu} (n)$.