Graphes Aléatoires Hyperboliques

Pendant un stage de 4 mois (avril à juillet 2018) en fin de M1, j’ai étudié des modèles de propagation dans les graphes aléatoires hyperboliques (Random Hyperbolic Graphs, noté RHG), au laboratoire J.A. Dieudonné (Université Nice Côte d’Azur). J’étais encadré par Dieter Mitsche.

Graphes aléatoires hyperboliques

Les RHG sont une généralisation des graphes aléatoires géométriques à des espaces hyperboliques. Les graphes aléatoires géométriques ont des points uniformément générés dans une partie de l’espace euclidien et deux sommets sont connectés par une arête si la distance euclidienne entre eux est inféreieur à un certain seuil qui est un paramètre du modèle. Les arêtes des RHG sont générés selon la même règle, sauf que la distance utilisée est la distance hyperbolique $\text{dH}$ dans un espace hyperbolique de courbure négative.

Soit $\alpha, \nu > 0$ et $n \in \mathbb{N}$. Fixant $R := 2 \log (n / \nu)$, on dit que le graphe $\mathcal{G}_{\alpha, ~\nu} (n) := (V, E)$ (with $|V| = n$) est un RHG si :

• les sommets $v_1, \dots, v_n$ de $V$ sont indépendamment dans $\mathbb{B}(O, R)$ avec densité $$ f: \mathbb{R}_+ \times [0, 2\pi[ \to \mathbb{R}, \quad (r, \theta) \mapsto \frac{\rho(r)}{2\pi} \quad \text{où} \quad \rho(r) = \frac{\alpha \sinh(\alpha r)}{\cosh(\alpha R) - 1} \textbf{1} (r \in [0, R])$$ (ce qui signifie que les coordonnées radiales et angulaires $r$ et $\theta$ d’un sommet sont indépendantes, $r$ genéré avec densité $\rho$ et $\theta$ choisi uniformément dans $[0, 2\pi[$).

• l’ensemble des arêtes $E$ est entièrement déterminé par la position des sommets, puisque deux sommets $u, v \in V$ sont adjacents si et seulement si $\text{dH} (u, v) \leq R$: $$ u \leftrightarrow v \in E \quad \Leftrightarrow \quad \text{dH} (u, v) \leq R $$

Propagation Push & Pull

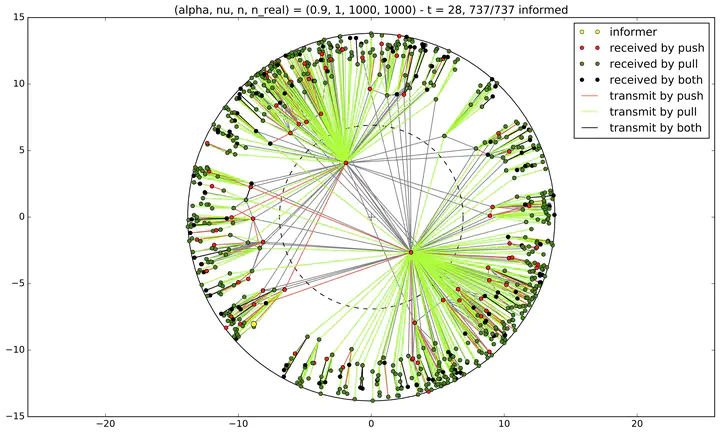
J’ai étudié un modèle de propagation de rumeur appelé push & pull. La propagation commence par informer un sommet aléatoire à l’instant initial $t=0$, puis à chaque pas de temps deux procesus indépendants ont lieu simultanément :

• un push : chaque sommet informé choisi l’un de ses voisins uniformément et lui transmets l’information s’il ne l’avait pas encore,
• un pull : chaque sommet non informé choisi l’un de ses voisins uniformément. Si celui-ci est déjà informé, il devient aussi informé.

Notre but était de trouver le temps moyuen nécessaire pour informer l’ensemble des sommets de la composante géante de $\mathcal{G}_{\alpha,~\nu} (n)$.